Sup guys! Just like what we did for Science, we’ve gone through 2025 WA1 Maths papers from different schools to spot the trendiest and trickiest questions.
Below, we’ll run through our Maths problem-solving strategies and Power Codes to help you solve each problem — step by step, no stress. Our Maths WA1 Annotated Solutions Guide includes detailed walk-throughs for all the questions. Take some time to go through them, it’ll definitely help!
Trending Question Types
There are two question types that are trending in 2025:
Example 1: Unchanged Total in Ratio
‘In a singing class, the students were split equally into two teams. The number of boys in Team A was 1/3 the number of girls in Team A. The ratio of the number of boys to the number of girls in Team B was 3 : 2. What is the ratio of the number of boys to the number of girls in the singing class?’
In solving this question, students are expected to recognise that the total number of students in each group are the same. This allows us to apply an “Unchanged Total” problem-solving strategy to tackle this problem.
Using our Power Code Approach, we will:
Apply the least common multiple (LCM) to make total units the same for Team A and B (Team A: 20 units and Team B: 20 units),
Then adjust the units for boys and girls in Team A and B accordingly, Team A: Boys (5 units), Girls (15 units), Team B: Boys (12 units), Girls (8 units)
Finally, we will simplify to the required ratio of 17 : 23.
Example 2: Excess and Shortage
‘John has some sweets for a group of students. If each student receives 7 sweets, he will have 5 sweets left. If each student receives 9 sweets, he will need another 7 more sweets. (a) How many students are there? (b) How many sweets does John have?’
Students are expected to recognise that there are two different scenarios in this question, of which the first scenario will result in an excess of sweets (“5 leftover”), while the second will result in a shortage (“need another 7”). This allows us to apply an “Excess and Shortage” Power Code to solve this question.
We simplify the problem by setting up a clear table using the listing method to find the first common number that appears in both scenarios.
Here are two stretch questions to challenge yourself with:
Example 1
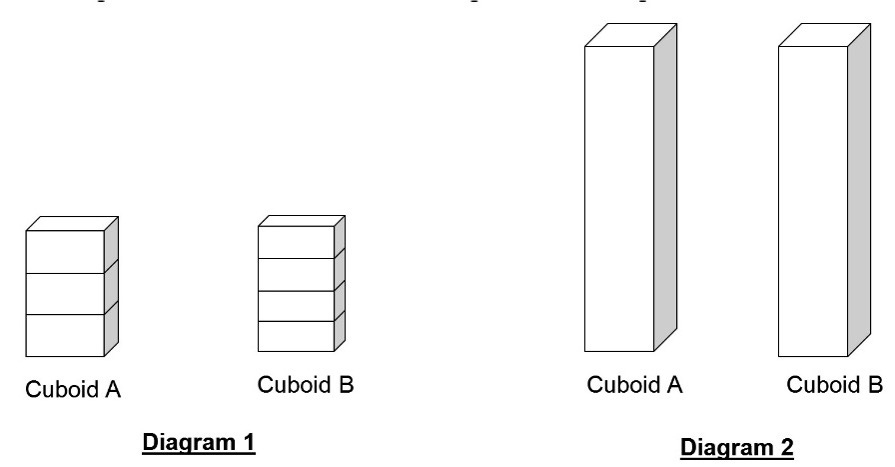
‘Jane had two different types of cuboids, A and B with different height. The height of 3 Cuboid A is the same as height of 4 Cuboid B in Diagram 1. Diagram 2 displays an unknown number of Cuboid A stacked at the same height as an unknown number stack of Cuboid B. Each Cuboid A and B weighs 36 g and 24 g respectively. The total weight of the 2 stacks of cuboids in Diagram 2 is 40.8 kg.’
Most students often struggle with this type of problems due to challenges in interpreting the relationship between the number of cuboids (3 Cuboid A = 4 Cuboid B) and the link between the total weight of the cuboids and the number of cuboids.
Our Make A Set techniques simplifies it by:
First grouping 3 Cuboid A and 4 Cuboid B into a single set,
Calculating the weight of one set (204 g), and then
Finding the number of sets (20) needed to match the total weight of 40,800 g.
This structured approach reorganises the problem by helping students to systematically calculate the required values without getting overwhelmed by it.
Example 2
‘Mrs Wong spent 2/5 of her money on 5 identical erasers and 9 identical rulers. The cost of one ruler is thrice the cost of one eraser. She bought more erasers with 1/2 of her remaining money. How many erasers did Mrs Wong buy altogether?’
Students face difficulty with this problem because they misinterpret the fractions of money spent (2/5 initially, then 1/2 of the remaining). They also fail to recognise the relationship between ruler and eraser (1 ruler = 3 erasers). This question is more challenging, as it incorporates two different problem-solving strategies.
Our Simplify the Problem and Fraction of a Remainder techniques guide students to systematically solve this problem:
First, simplify the problem by converting the cost of rulers into an equivalent number of erasers (9 rulers = 27 erasers);
Then, to calculate the total erasers that can be bought with 2/5 of Mrs. Wong’s money (32 erasers);
This allows us to find the additional erasers that can be bought (24 more) with half of her remaining money, by applying fraction of remainder.
Common Misconceptions & Mistakes (with Tips to Avoid)
Here are two common mistakes to avoid:
Mistake 1: Conceptual Errors
‘A shirt costs $40, and its price is increased by 20%. What is the new price?’
Some students mistakenly calculate 20% of the original price as the new price, getting $8, instead of adding the increase to the original price. They attempt to solve problems by relying on memorised procedures without fully understanding the underlying concepts, leading them to apply incorrect methods to similar-looking questions.
Tip: Underline/highlight key information. Annotate to make sure you understand key information. Read and re-read the question.
Mistake 2: Misreading Units
'A tank fills at 2 L/min under a running tap, while a hole allows water to leak at 500 mL/min at the same time. How much remains after 3 minutes?'
Some got 45 L instead of 4.5 L, forgetting 500 mL = 0.5 L (6 L in, 1.5 L out).
Tip: Underline units in the question, convert them to the same units before calculating, and recheck your answer matches the unit asked. Practice this habit, and it’ll stick! 💪🏼
